
Reading instruction was once a topic guaranteed to ignite passionate debate among teachers, mostly between proponents of phonics instruction and supporters of whole-language approaches. Although this particular controversy has become less heated in recent years, with many endorsing a hybrid or mixed-methods approach, there remains a great deal of interest in the relative merits of the various approaches to reading instruction; and, by extension, treatment of reading disability.
It’s not surprising that the topic attracts so much attention. Reading disability is common, with the NHS estimating an incidence rate as high as 10%; it affects student performance in virtually all academic areas; and it can affect self-esteem well into adulthood. Fortunately, there are many treatment options. Knowing which are worth using requires an understanding of their effectiveness in a controlled research environment. Four researchers from Germany have weighed in with a recent meta-analysis. They concluded that only phonics instruction could be proven effective. Interestingly, it doesn’t necessarily follow that other treatments are ineffective, or even less effective. Intrigued? Read on for details.
The Evidence
In February 2014, a meta-analysis of treatment approaches for children and adolescents with reading disability was published in the peer-reviewed open-access journal PLoS One.
The researchers had two aims:
- To establish the effectiveness of different treatments for children and adolescents with reading disability
- To look at the impact of various factors on treatment effectiveness
Methods
The meta-analysis included only randomised controlled trials (RCTs): studies in which half the participants were randomly assigned to treatment, and the other half given no treatment or a placebo treatment. Screening criteria included quality control measures. In addition, study participants had to have:

The reviewers pooled the results from 22 randomised controlled trials to ascertain which method was best for treating reading disability
- Reading performance that was one year, one grade, one standard deviation or more below the expected level; or below the 25th percentile. The language in which participants had difficulty had to be their mother tongue
- Intelligence in the normal range
The researchers ultimately included 22 studies, which together yielded 49 comparisons of treatments with non-treatments or placebos. All used pre- and post-tests of reading and/or spelling to assess treatment effectiveness. Treatments were divided into seven categories:
- Phonemic awareness instruction
- Phonics instruction
- Reading fluency training
- Reading comprehension training
- Auditory training
- Medical treatment
- Coloured overlays
Detailed definitions are given in the meta-analysis (scroll to ‘Coding of the RCTs’). The researchers used accepted statistical methods to pool and analyze the results of all studies within each treatment category. Sub-group analyses were used to assess the impact of various factors on treatment effectiveness.
Effect sizes and confidence intervals
A treatment that consistently improves reading performance by a tiny fraction of a grade level might technically be effective, but few education professionals would have much praise for it. Fortunately, the researchers doing this meta-analysis follow standard practice by reporting mean effect size for each treatment. Effect sizes measure the amount of difference a treatment makes. In education, an effect size as small as 0.2 may be of interest to policy makers (Hedges & Hedberg, 2007).
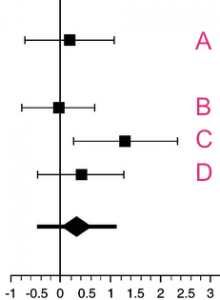
Figure 1: Only result C on this graph is statistically significant, because the confidence interval does not go below zero
It’s possible, however, that some of the change in the performance of our random sample (i.e., the effect size) will be the result of chance. This is taken into account through a second figure, the confidence interval, which usually looks something like this: CI 95% (-0.6 to 1.3).
Figure 1 presents this calculation in result D which shows the effect size of 0.5 and a confidence interval from -0.6 to 1.3. This means that we think the most likely effect size is 0.5, but it could be as low as -0.6 or as high as 1.3.
It’s important to note that a confidence interval that goes below zero indicates a result that is not statistically significant. The only statistically significant row in figure 1 is result C, which could also be written as Effect size = 1.3 (CI 95%, 0.3 to 2.4).
This is a simplification that will make statisticians cringe, but for our purposes, it will do. See the Statistics Glossary for a more extensive explanation of confidence intervals.
Results
Phonics instruction was the only treatment proven to have a statistically significant effect on reading and spelling performance. Here are the details of the researchers’ findings on reading performance:
- Phonemic awareness instruction (3 comparisons):
- Effect size (ES) 0.279
- Confidence Interval 95% (-0.244 to 0.802) statistically insignificant

Phonics instruction was the only treatment proven to have a statistically significant effect on reading and spelling performance.
- Phonics instruction (29 comparisons):
- ES = 0.322
- CI 95% (0.177 to 0.467) statistically significant
- Reading fluency training (5 comparisons):
- ES = 0.301
- CI 95% (-0.105 to 0.707) statistically insignificant
- Reading comprehension training (3 comparisons):
- ES = 0.177
- CI 95% (-0.181 to 0.535) statistically insignificant
- Auditory training (3 comparisons):
- ES = 0.387
- CI 95% (-0.065 to 0.838) statistically insignificant
- Medical treatment (2 comparisons):
- ES = 0.125
- CI 95% (-0.322 to 1.331) statistically insignificant
- Coloured overlays (4 comparisons):
- ES = 0.316
- CI 95% (-0.012 to 0.644) statistically insignificant
There weren’t enough studies looking at spelling performance to calculate mean effect sizes for any treatments except phonics, for which there was a small but significant effect. As you can see from the number of comparisons, there were considerably more trials of phonics than the other treatments.
The researchers concluded that their examination of factors influencing treatment effectiveness ‘do not allow clear conclusions about what makes an intervention successful’. Results did suggest that severity of reading disability might affect response to treatment, with those with milder disability seeing greater improvement.
Conclusions
The reviewers conclude:
Phonics is the most intensively investigated treatment approach. In addition, it is the only approach whose effectiveness on reading and spelling performance in children and adolescents with reading disabilities is statistically confirmed.
They also state that:
At the current state of knowledge, it is adequate to conclude that the systematic instruction of letter-sound-correspondences and decoding strategies, and the application of these skills in reading and writing activities [i.e., phonics training], is the most effective method for improving literacy skills of children and adolescents with reading disabilities.
The first conclusion is well supported by the evidence. The second conclusion, in my opinion, is questionable.
Summary
This well-reported and statistically rigorous meta-analysis has one shortcoming: the authors don’t fully address the implications of the disproportionately large number of phonics trials (29 vs. <6 for all other treatments). Total sample sizes for each treatment aren’t reported, but it seems safe to assume that the group of participants receiving phonics instruction was the largest by far.
Confidence intervals are a function of sample size and effect size. The larger the study sample (in this case, the more people receiving a particular treatment) the more sure we can be that the results we see aren’t due to chance. Imagine flipping a coin four times and getting three heads, one tail. “This coin is fixed!” says your friend. “Don’t be ridiculous,” you say. “That doesn’t prove anything.” Your friend persists, however, and you (with considerable reluctance) flip the coin ninety-six more times. To your surprise, heads comes up 75 times, tails 25 times. At this point, you are far more willing to concede that something might be amiss.

Adding new research to an updated version of this review may show that other treatments are also effective
This suggests that we must be careful about what claims this meta-analysis can and cannot support. The meta-analysis did not compare treatments with each other; it compared each treatment with non-treatment or a placebo. If we return to the bulleted list in the ‘Results’ section, we see that auditory training actually had a larger effect size (0.387) than phonics instruction (0.322). However, the sample of participants undergoing auditory training was quite small and the confidence interval is therefore quite large, rendering the effect statistically insignificant.
Does this mean that we could prove that auditory training was as good than phonics instruction, if only we had a larger sample? No. It means that we can’t tell, just as we can’t conclude whether a coin is fixed on the basis of four flips. The fact that phonics was the only treatment to emerge as having a statistically significant effect was partly a consequence of the fact that the phonics group of studies had enough ‘coin flips’ to allow us to demonstrate that its effect was very unlikely to be due to chance.
Take-away message
- Phonics is the only treatment that has been proven effective for treating reading disability
- It may or may not be more effective than other treatments
- We need more well conducted randomised controlled trials to provide a reliable answer to this question
Links
Galuschka K, Ise E, Krick K, Schulte-Korne G. Effectiveness of treatment approaches for children with reading disabilities: a meta-analysis of randomized controlled trials. PLOS One 2014; 9(2): e89900.
Easton, VJ and McCall, JH. “Confidence Interval”. University of Glasgow Statistics Glossary, 1997.
Understanding, using, and calculating effect size (PDF). Government of South Australia, Department of Education and Child Development.
Hedges LV, Hedberg E. Interclass correlation values for planning group-randomized trials in education (PDF). Educational Evaluation and Policy Analysis 2007 29(1): 60–87.
Dyslexia – Overview. NHS Choices, 2014.

Systematic Review: Phonemic awareness instruction ineffective for treating reading disability: http://t.co/nYhCYIv4Hg
Phonics instruction was only treatment proven to have statistically significant effect on reading & spelling problems http://t.co/mYWScKIMZb
Phonics is the only treatment proven effective for reading disability, but is that just because it has more trials? http://t.co/mYWScKIMZb
Teachers! Do you struggle with effect sizes & confidence intervals? There’s a handy tutorial in our blog today: http://t.co/mYWScKIMZb
Alison Jones summarises a meta-analysis of treatment approaches for children & adolescents with reading disability http://t.co/mYWScKIMZb
Only phonics instruction is proven effective for treating reading disability, says systematic review http://t.co/HwzRdogDva via @sharethis
Don’t miss: Only phonics instruction is proven effective for treating reading disability, says systematic review http://t.co/mYWScKIMZb
When I was a literacy tutor for adults, I began as a volunteer, and it was mainly a whole language approach. Later I began a private practice and ended up incorporating more phonics. I saw a greater improvement with the adults that I used the phonics approach with.
In case you missed it: Only phonics instruction is proven effective for reading disability, says systematic review http://t.co/mYWScKIMZb
RT Only phonics instruction is proven effective for treating reading disability http://t.co/zsuTpEAhGU @juditkormos @pizornka @Mateja07
These findings are indicative for groups; for a particular student with problems at the neurological readiness level phonetic analysis for reading will not be enough. Phonetic reading is not a cure-all. Consider the 9th-grader receiving 6 years of phonetic reading intervention with an overlooked severe lack of auditory discrimination ability. Reading instruction may not be a treatment, but merely an intervention. Reading instruction is an academic activity that should be included in all cases of reading disability, but it is not a substitute for addressing neurodevelopmental problems. Reading instruction compared to non-reading interventions is a straw-man conversation. Teach reading and consider neuro-readiness for reading as pre-remedial reading intervention. Individualization is key to special needs. A single approach is a disaster for a certain proportion of any population.
i found this really interesting here I will finding out some more about this as I’m hooping to get a job at a school just for a few hours a week as I enjoy working with children with special needs as I learnt so much as I have a son with problems as well.
So thank you for al this information